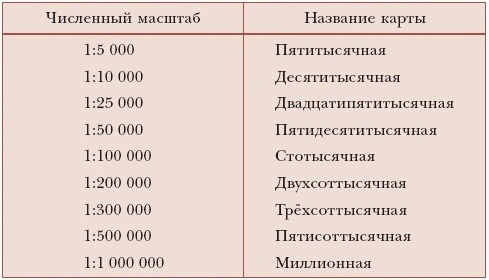
I. Прямо пропорциональные величины.
Пусть величина y зависит от величины х. Если при увеличении х в несколько раз величина у увеличивается во столько же раз, то такие величины х и у называются прямо пропорциональными.
Примеры.
1. Количество купленного товара и стоимость покупки (при фиксированной цене одной единицы товара — 1 штуки или 1 кг и т. д.) Во сколько раз больше товара купили, во столько раз больше и заплатили.
2. Пройденный путь и затраченное на него время (при постоянной скорости). Во сколько раз длиннее путь, во столько раз больше потратим времени на то, чтобы его пройти.
3. Объем какого-либо тела и его масса. (Если один арбуз в 2 раза больше другого, то и масса его будет в 2 раза больше)